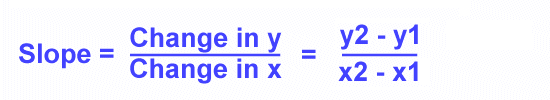Kids Math
Slope
In math, the slope describes how steep a straight line is. It is sometimes called the gradient.
Equations for Slope
The slope is defined as the "change in y" over the "change in x" of a line. If you pick two points on a line --- (x1,y1) and (x2,y2) --- you can calculate the slope by dividing y2 - y1 over x2 - x1.
Here are the formulas used to find the slope of a line:
Examples:
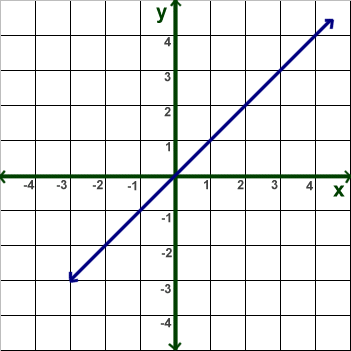
1) Find the slope for the line in the graph below:
This line goes through the points (0,0) and (3,3).
Slope = (y2 - y1)/(x2 - x1)
= (3 - 0)/(3 - 0)
= 3/3
= 1
This line has a slope of 1. Try using different points on the line. You should get the same slope regardless of what points you use.
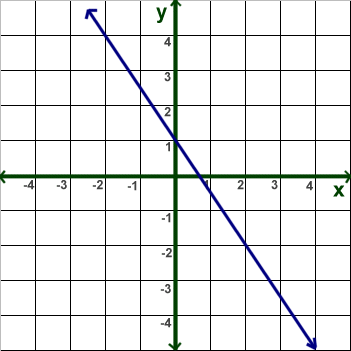
2) Find the slope of the line in the graph below:
You can see that the line contains the points (-2,4) and (2, -2).
Slope = (y2 - y1)/(x2 - x1)
= (-2 - 4))/(2 - (-2))
= -6/4
= - 3/2
Special Cases
Some special cases include horizontal and vertical lines.
A horizontal line is flat. The change in y is 0, so the slope is 0.
A vertical line has a change in x of 0. Since you can't divide by 0, a vertical line has an undefined slope.
Up or Down - Positive or Negative Slope
If you look at the line from left to right, a line that is moving up will have a positive slope and a line that is moving down will have a negative slope. You can see this on the two example problems above.
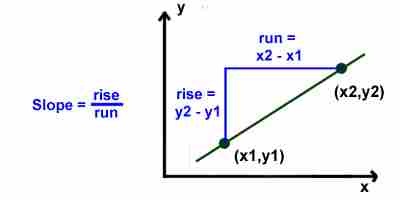
Rise over Run
Another way to remember how the slope works is "rise over run". You can draw a right triangle using any two points on the line. The rise is the distance that the line travels up or down. The run is the distance that the line travels from left to right.
Things to Remember
- Slope = change in y over the change in x
- Slope = (y2 - y1)/(x2 - x1)
- Slope = rise over run
- You can pick any two points on a line to calculate the slope.
- You can double check your answer by trying different points on the line.
- If the line is going up, from left to right, the slope is positive.
- If the line is going down, from left to right, the slope is negative.
More Geometry Subjects
Circle
Polygons
Quadrilaterals
Triangles
Pythagorean Theorem
Perimeter
Slope
Surface Area
Volume of a Box or Cube
Volume and Surface Area of a Sphere
Volume and Surface Area of a Cylinder
Volume and Surface Area of a Cone
Angles glossary
Figures and Shapes glossary
Back to Kids Math
Back to Kids Study