Kids Math
Finding the Volume and
Surface Area of a Cone
What is a cone?
A cone is a type of geometric shape. There are different kinds of cones. They all have a flat surface on one side that tapers to a point on the other side.
We will be discussing a right circular cone on this page. This is a cone with a circle for a flat surface that tapers to a point that is 90 degrees from the center of the circle.
Terms of a Cone
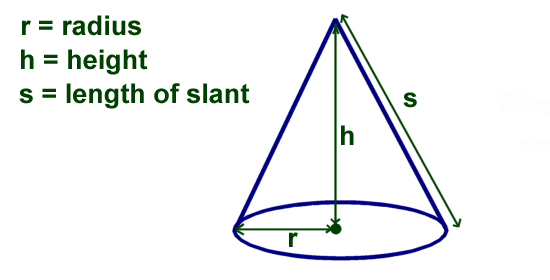
In order to calculate the surface area and volume of a cone we first need to understand a few terms:
Radius - The radius is the distance from the center to the edge of the circle at the end.
Height - The height is the distance from the center of the circle to the tip of the cone.
Slant - The slant is the length from the edge of the circle to the tip of the cone.
Pi - Pi is a special number used with circles. We will use an abbreviated version where Pi = 3.14. We also use the symbol π to refer to the number pi in formulas.
Surface Area of a Cone
The surface area of a cone is the surface area of the outside of the cone plus the surface area of the circle at the end. There is a special formula used to figure this out.
Surface area = πrs + πr2
r = radius
s = slant
π = 3.14
This is the same as saying (3.14 x radius x slant) + (3.14 x radius x radius)
Example:
What is the surface area of a cone with radius 4 cm and slant 8 cm?
Surface area = πrs + πr2
= (3.14x4x8) + (3.14x4x4)
= 100.48 + 50.24
= 150.72 cm2
Volume of a Cone
There is special formula for finding the volume of a cone. The volume is how much space takes up the inside of a cone. The answer to a volume question is always in cubic units.
Volume = 1/3πr2h
This is the same as 3.14 x radius x radius x height ÷ 3
Example:
Find the volume of a cone with radius 4 cm and height 7 cm?
Volume = 1/3πr2h
= 3.14 x 4 x 4 x 7 ÷ 3
= 117.23 cm 3
Things to Remember
- Surface area of a cone = πrs + πr2
- Volume of a cone = 1/3πr2h
- The slant of a right circle cone can be figured out using the Pythagorean Theorem if you have the height and the radius.
- Answers for volume problems should always be in cubic units.
- Answers for surface area problems should always be in square units.
More Geometry Subjects
Circle
Polygons
Quadrilaterals
Triangles
Pythagorean Theorem
Perimeter
Slope
Surface Area
Volume of a Box or Cube
Volume and Surface Area of a Sphere
Volume and Surface Area of a Cylinder
Volume and Surface Area of a Cone
Angles glossary
Figures and Shapes glossary
Back to Kids Math
Back to Kids Study