|
|
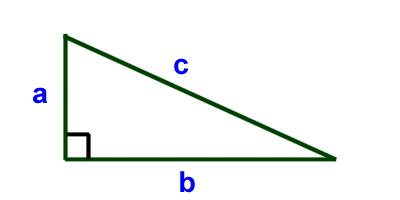
|
a2 + b2 = c2
32 + 42 = c2 3x3 + 4x4 = c2 9+16 = c2 25 = c x c c = 5 |
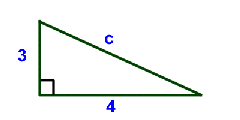
|
|
a2 + b2 = c2
a2 + 122 = 152 a2 + 144 = 225 Subtract 144 from each side to get: 144 - 144 + a2 = 225 - 144 a2 = 225 - 144 a2 = 81 a = 9 |
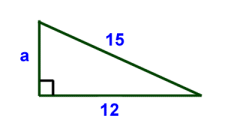
|
Back to Kids Math
Back to Kids Study