Kids Math
Finding the Volume and
Surface Area of a Sphere
What is a sphere?
A sphere is a three dimensional version of a circle, like a basketball or a marble. The definition of a sphere is "every point that is the same distance from a single point called the center."
Terms of a Sphere
In order to calculate the surface area and volume of a sphere we first need to understand a few terms:
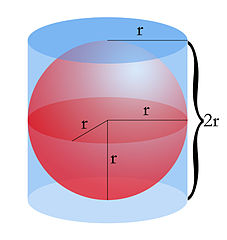
Radius - The radius of a sphere is the distance from the center to the surface. It will be the same distance for a sphere no matter where it is measured from the surface.
Diameter - The diameter is a straight line from one point on the surface of the sphere to another that goes through the center of the sphere. The diameter is always twice the distance of the radius.
Pi - Pi is a special number used with circles and spheres. It goes on forever, but we will use an abbreviated version where Pi = 3.14. We also use the symbol π to refer to the number pi in formulas.
Surface Area of a Sphere
To find the surface area of a sphere we use a special formula. The answer to this formula will be in square units.
Surface Area = 4πr2
This is the same as saying: 4 x 3.14 x radius x radius
Example Problem
What is the surface area of a sphere that has a radius of 5 inches?
4πr2
= 4 x 3.14 x 5 inches x 5 inches
= 314 inches2
Volume of a Sphere
There is another special formula for finding the volume of a sphere. The volume is how much space takes up the inside of a sphere. The answer to a volume question is always in cubic units.
Volume = 4/3 πr3
This is the same as 4 ÷ 3 x 3.14 x radius x radius x radius
Example Problem
What is the volume of a sphere with a radius of 3 feet?
Volume = 4/3 πr3
= 4 ÷ 3 x 3.14 x 3 x 3 x 3
= 113.04 feet3
Things to Remember
- Surface area of sphere = 4πr2
- Volume of a sphere = 4/3 πr3
- You only need to know the radius to figure both the volume and surface area of a sphere.
- Answers for surface area problems should always be in square units.
- Answers for volume problems should always be in cubic units.
More Geometry Subjects
Circle
Polygons
Quadrilaterals
Triangles
Pythagorean Theorem
Perimeter
Slope
Surface Area
Volume of a Box or Cube
Volume and Surface Area of a Sphere
Volume and Surface Area of a Cylinder
Volume and Surface Area of a Cone
Angles glossary
Figures and Shapes glossary
Back to Kids Math
Back to Kids Study