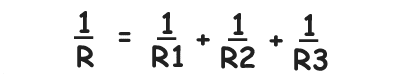Circuits and Components
Intro to Electricity
Electric Circuits
Electric Current
Ohm's Law
Resistors, Capacitors, and Inductors
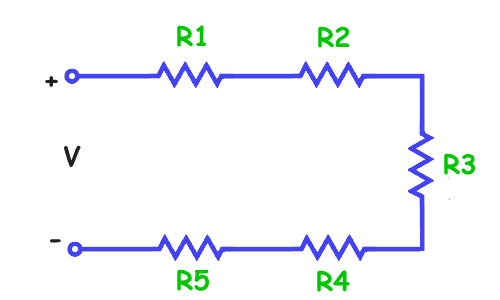
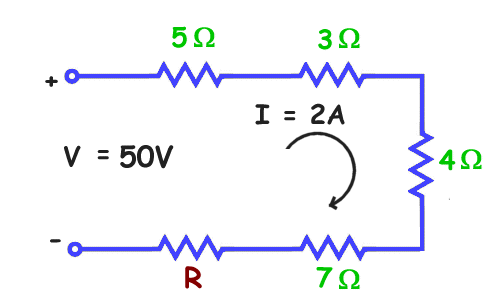
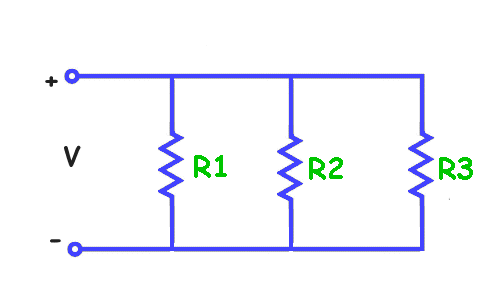
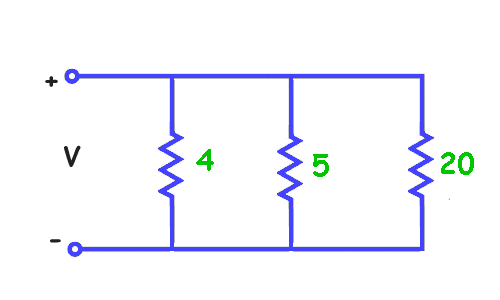
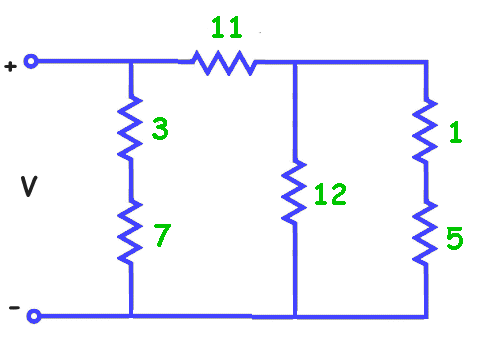
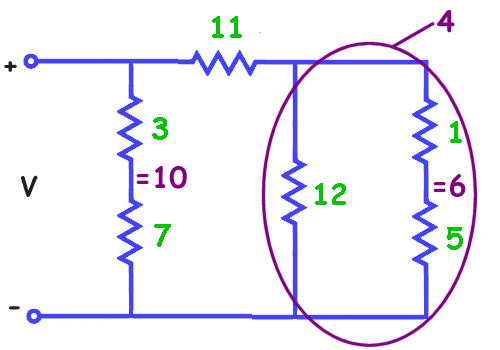
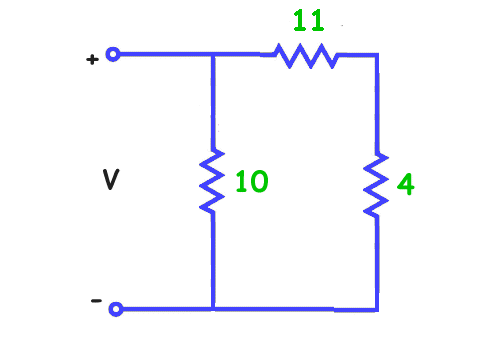
Resistors in Series and Parallel
Conductors and Insulators
Digital Electronics
|
Other Electricity
Electricity Basics
Electronic Communications
Uses of Electricity
Electricity in Nature
Static Electricity
Magnetism
Electric Motors
Glossary of Electricity Terms
|