|
Kids Math
Triangles
|
|
Triangles are three sided polygons. One of the interesting things about triangles is that if you sum up the three angles within any triangle, they will always total 180 degrees. This comes in handy when working geometry problems.
There are several types of triangles. Some triangles can be described by their sides, like the equilateral, isosceles, and scalene. Some triangles are described by their angles like the right triangle, obtuse, and acute.
Equilateral Triangle
|
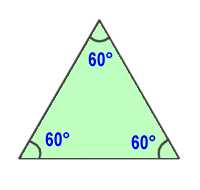
The equilateral triangle is a triangle with sides that are all the same length. The three angles are all the same too. If we use what we learned above, that all the angles must total 180 degrees, then each angle in an equilateral triangle is 180/3 = 60 degrees.
|
|
Isosceles Triangle
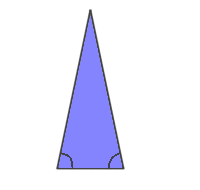
| An isosceles triangle is a triangle with two equal sides. As a result of having two equal sides, two of the angles will be the same too. |
|
Scalene Triangle
A scalene triangle is one where none of the sides are the same length.
Right Triangle
The right triangle is one where one of its angles is 90 degrees. This type of triangle has some unique properties that are important to geometry including the Pythagorean Theorem. Triangles that are not right triangles, or don't have an angle of 90 degrees are called oblique.
Acute Triangle
An acute triangle is a triangle where all the interior angles are less than 90 degrees.
Obtuse Triangle
An obtuse triangle is the opposite of an acute triangle in that it is a triangle where at least one angle is greater than 90 degrees.
Acute and obtuse triangles are both oblique.
Fun Facts about Triangles
- Triangles are becoming used more in construction. They are harder to use than rectangles, but can be stronger and may be more resistant to earthquakes.
- If you draw a line in a rectangle from far corner to corner you cut the rectangle into two right triangles.
- If you know two of the angles in a triangle, you can always figure out the third because they must add up to 180 degrees.
- The sum of the lengths of any two sides of a triangle is always longer than the third side.
- The triangle and two is a type of defense used in basketball.
- In North Carolina there are three cities: Raleigh, Durham, and Chapel Hill, that are often referred to as The Triangle.
Advanced Kids Math Subjects
Statistics
Mean, Median, Mode, and Range
Picture Graphs
Algebra
Order of Operations
Exponents
Ratios
Ratios, Fractions, and Percentages
Geometry
Polygons
Quadrilaterals
Triangles
Pythagorean Theorem
Circle
Perimeter
Surface Area
Misc
Prime Numbers
Roman Numerals
Back to Kids Math
Back to Kids Study
|
|
Kid's Poll |
|
Which of these cities would you most like to visit on vacation?
|
|
Joke of the Day |
Q: Knock, knock----Who's There?----Ashe----Ashe who?
A: Bless you!
|
|
Today In History |
|
Who was born on this day:
1952 Mr. T (Actor)
1981 Josh Hamilton (Baseball player)
What happened today in history:
1881 The American Red Cross is established by Clara Barton.
1927 Charles Lindbergh completes the first solo nonstop flight across the Atlantic Ocean.
|
|
